すなわち,上記の偏心(a,b)を決定し,それを中心と した同心円でワーク形状を挟んだ場合の半径差が真円度と なることを意味している. 5.真円度と基準円 真円度の求め方には,基準円を元に以下の4つの方法が ある3). 1.最小領域真円度/最小領域基準円 3次元空間での円の中心の求め方 年6月12日 / 最終更新日時 年6月12日 iNak Eng CEO VBNet 前回のコラムがくだけすぎでしたので、今回はまともなロジックを取り上げます。Re円の座標の求め方 投稿記事 by 2³ » 1 year ago 僕はC#使ってるのでC#での説明になってしまいますが、 vx = (float)MathCos (rad) * r ox;

中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット
円 中心 求め方 公式
円 中心 求め方 公式- 更新 1254 編集 jdash00 概要 円弧の一部から円の中心を見つけることができるのはなぜなのかを作図ソフトのIllustratorを使って考えてみました。 「 正確に円弧をトレースするためのTips DTP Transit 」を読んでいて、正直何をしているのか意味が 中心角 = 360× 半径 母線 中 心 角 = 360 × 半 径 母 線




3点を通る円を求める Qiita
課題 2 必要な流量を流すために設定しなければならない水路の勾配を求めてみよう。 計算の手順 手順1 計算に必要な、水路の断面形状のデーターと勾配のデーターを整理しよう。 水路の直径、中心角(水深が与えられている場合は課題1の方法で中心角を求める。 こんにちは、ウチダです。 今日は数学a「図形の性質」で習う 「三角形の内心」 について、性質の証明や基本的な使い方(角の二等分線と比)、座標の求め方や位置ベクトル表示などをわかりやすく解説していきたいと思います。 外心に関する記事と内容がかなり似ているため、こちらの記事右図5において,原点を中心とする半径5の円の方程式を求めてみよう. 円周上の点 P の座標を (x , y) とおくと,ピタゴラスの定理(三平方の定理)により, x 2 y 2 =5 2 (A) が成り立つ. 上半円については, y ≧ 0 なので, y= (B)
例題 上節でみたように,$2$ 円の位置関係を調べるには,$2$ つの円の半径と,中心間の距離を調べればよいのでした.円の方程式からその中心の座標と半径を求める方法は前記事 →円の方程式の表し方 で紹介しています.これらの知識を用いて,実際にいくつかの例題を解いてみましょう.指定した3点を通る円の式 困っていたのでありがたいです。 計算過程も書いてあると尚嬉しいです。 タンクの中心からずれた位置へ差し込むパイプの長さを求めました。 半径rと x座標a,c,e から y座標b,d,f が求められればサイコーです! アンケートにごVy = (float)MathSin (rad) * r oy;
円を選択する 円弧の選択を考える前に、円をマウスで選択することを考えます。 ここでいう選択は、円内部点ではなく、円周上をクリックしたとき「選択された」と考えます。 半径 R、中心点(Cx, Cy)の円を考えます。 これは簡単ですね。 中心角の作り方がわかったところで、もう一回先ほど定義を見てみましょう。 円の中心核の定義は、 「弧の両端を通る2つの半径の作る角」 でしたね。 この「2つの半径の作る角」のところは、②と③で確認した部分のことです。円の中心、半径を求める練習問題! まとめ 中3受験生へこの力を身につけたら本番で60点は楽勝にとれる! こちらの関連記事はいかがでしょうか?




中学数学 3点を通る円の中心の書き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
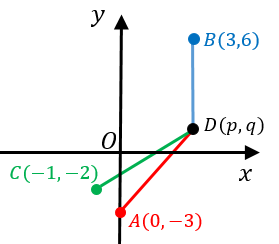



3点を通る円の方程式の2通りの求め方と検算方法 具体例で学ぶ数学
中心(a,b)で半径r、円周の任意の点を(x i,y i)とすると円は以下の式で表せます。 rと中心とx i,y i 間の距離の差を出す式をとりあえず差を0として作成します。 上記の式を二乗すると 左式を使って上式からカッコを取り除きシンプルにします。 円の方程式は、 (x-x0)^2 + (y-y0)^2 = r^2円の中心点を簡単に出す使い方 円の中心点を求めることも図面作成中によくあることだと思います。 円の中心点を出すのは、以外と難しいものでそう簡単には出すことができません。 しかし、Jw_cadなら数クリックで簡単に出すことができる機能が備わって
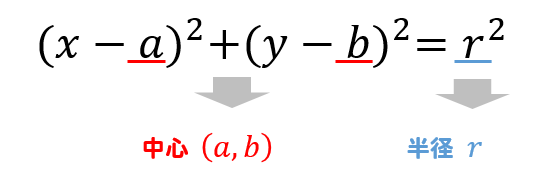



円の方程式 中心の座標と半径の求め方を解説 数スタ




基本 円の方程式 なかけんの数学ノート
円の確認 円の方程式~基本形(標準形)と一般形 円の方程式の決定(中心と半径など) 円の方程式の決定(通る3点など) 円と直線の位置関係 円と直線の方程式を連立してできる2次方程式ax bx c2 0 の 判別式D b ac 2 4 に注目すると,次のようになる。 3点を通る円の作図の考え方としては 円の中心を求める⇒中心にコンパスの針を置いて円をかく という手順になります。 それでは、先ほどの問題と同じように 円の中心を求めていきましょう。 3点のうち2組の垂直二等分線をかきます。 球の中心の求め方 前回のコラムで3次元空間での円の中心の求め方について記述したので、次に空間内にある球の中心を求めるロジックについて考えてみます。 球については、表面上にある4点の座標が指定されたら形状が確定します。 (3点の座標と半径




中1 作図 円の中心を求める方法を解説 数スタ




円周の求め方 公式は直径を使うので 半径と間違えないように 中学や高校の数学の計算問題
円の面積の求め方 円の面積を求めるときは 円の面積 = 半径 × 半径 × 円周率 という公式を使います。 たとえば、半径が 3 c m の円の面積は 半径 半径 円周率 半 径 × 半 径 × 円 周 率 = 3 × 3 × 314 = 26 c m 2 と求めることができます。 pYの値も解り、円の中心座標 P(pX,pY)が解るw 上記の写真を例に円の中心座標を求めてみるw A(aX,aY)=(1,1) B(bX,bY)=(5,5) C(cX,cY)=(15,5) っとしたとき、 ①②の式に当てはめてみると、 ①pX=(1^25^21^25^22pY(15))/2(15) → pX=6pY垂直2等分線 次のような問題があったとしましょう。 上の図において、円の中心oを図示しなさい。 このような問題の場合には、垂直2等分線を用いて中心oの位置を求めることができます。 垂直2等分線のおさらい 垂直2等分線とは、下図のよ
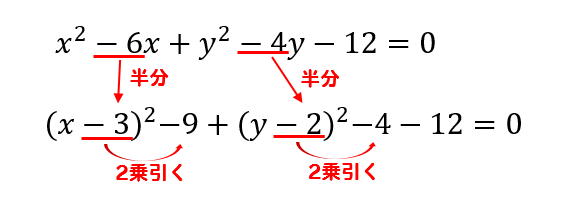



円の方程式 中心の座標と半径の求め方を解説 数スタ




三角形の外心について知っておきたい知識まとめ 理系ラボ
外接円、外心について 「外接円」や「外心」の用語や意味は中学の 教科書の発展内容としてあります。 それぞれの各辺の垂直二等分線は一点でまじわり、その点Dを中心に円を書くと Dを中心に三角形の3つの頂点を通る円を書くことができて、この円④No12以降の各中心杭までの弧長は、中心杭間距離000mを逐次加えて求め、それに対する偏 角は、中心点杭間距離に対する偏角δを、加えることにより求める。 例えば、No12の杭は、 ° ¢ ² ° ´ ´ = 5 43 57 314 180 2 m 000m δ= であるから、IPから 円の中心の求め方 数学 ケガキについて 工学 4 ミリのステンレスに穴を開けたい diy・エクステリア 5 作図により円の中心の求める方法について質問です。 ①ある円で任意の異なる4点a,b,c,dをとる。




差し金テク 円の中心と直径を限りなく正確に求める方法 男のレシピ帳
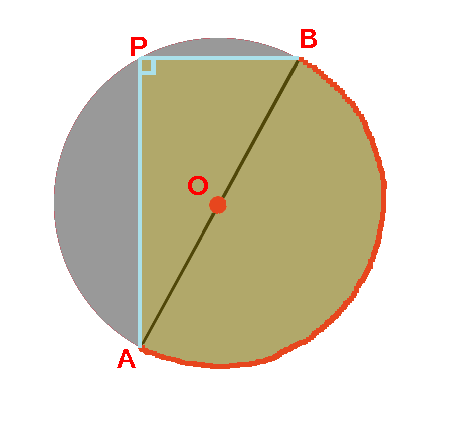



空き缶の中心の見つけ方 綿菓子を自宅で作ろう
包含円となりうるものは何通りあるか? u v 赤側 青側 u, v以外の点を直線uv に 関して2分割 赤側と青側 各点について,その点と u, vを通る円を求めたとき, 青側の点は,青側に中心 をもつ半径最大の円 質問74: 台風の中心位置の決め方 まず「台風の中心位置とは何か」という問題について考えましょう。 台風の中心位置の定義には以下のようなものがあります(他にもあるかもしれません)。 これらの基準によって決定される台風中心位置はそれぞれ外接円中心方式,内 接円中心方式および最小領域中心 方式は,い ずれも円形部分の輪郭図形を求めることが必 要である。また,平 均円中心方式でも輪郭に応じた電気 信号を求める必要がある。そこで,つ ぎに円形部分の輪 郭の求め方について述べる。




中学数学 円の中心の出し方 コンパス編 サクッとわかる なぜか分かる はかせちゃんの怪しい研究室




扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ
円 x^2y^2=r^2の傾きmの接線の方程式の求め方で よく点と線の距離公式を使った解き方をすると思うのですが 手持ちの公式集にy=mx±r√(m^2 1) と書いてあったのですが記述式の試験の場合この 方法で書いたら減点されるでしょうか 正直こっちの方法が楽なのですがでは,円の方程式の導き方を確認しましょう。 ここでは,『「円周上の点」と「中心」の距離』と『半径』が同じということを利用して,円の方程式を導いてみます。 さらに,この式を展開して整理すると, x 2 y 22ax2bya 2 b 2r 2 =0 となります。 こんにちは、ウチダです。 今日は数学a「図形の性質」で習う 「三角形の外心(垂心)」 について、性質の証明や座標の求め方、位置ベクトル表示などをわかりやすく解説していきたいと思います。 外心とは なぜ"外心"なのか、いきなり説明することは困難です。



円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典




3分で分かる 中心角の求め方ー公式とその証明 練習問題をわかりやすく 合格サプリ
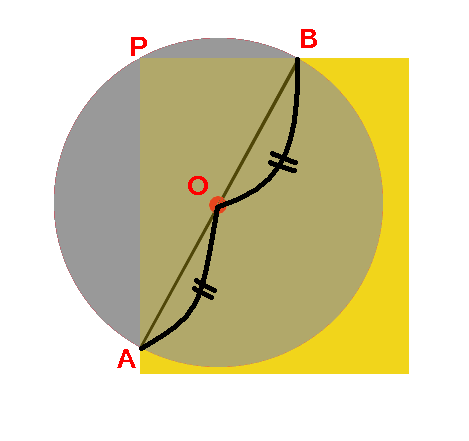
4、aとbを結んだ線の真ん中の点が、この円の中心になります。(oの点) 5、紙を空き缶に乗せて、求めた円の中心をクギなどで印を付ければできあがり! これは、円周角の定理を使った円の中心の求め方です。 円周角の定理とは 円周角の定理とは、図41 標準平歯車のかみあい (α=°、z 1 =12、z 2 =24、x 1 =x 2 =0) 上記計算は、歯車計算ソフト GCSW for Webで簡単に計算できます。 → こちら 表41 標準平歯車の計算 From灘 「円の中心の求め方」 – 朝日小学生新聞 中学受験eye 関西圏 From 進学校 16年9月5日 From灘 「円の中心の求め方」 私は現在、中学1年生に図形の性質を教えています。 定規とコンパスで図形をかく方法を説明した後に、「三角形ABCの三つの頂点を




最後の2円の中心間の距離の求め方が分かりません Clear




おうぎ形の中心角の求め方を詳しく教えてください お願いします Clear
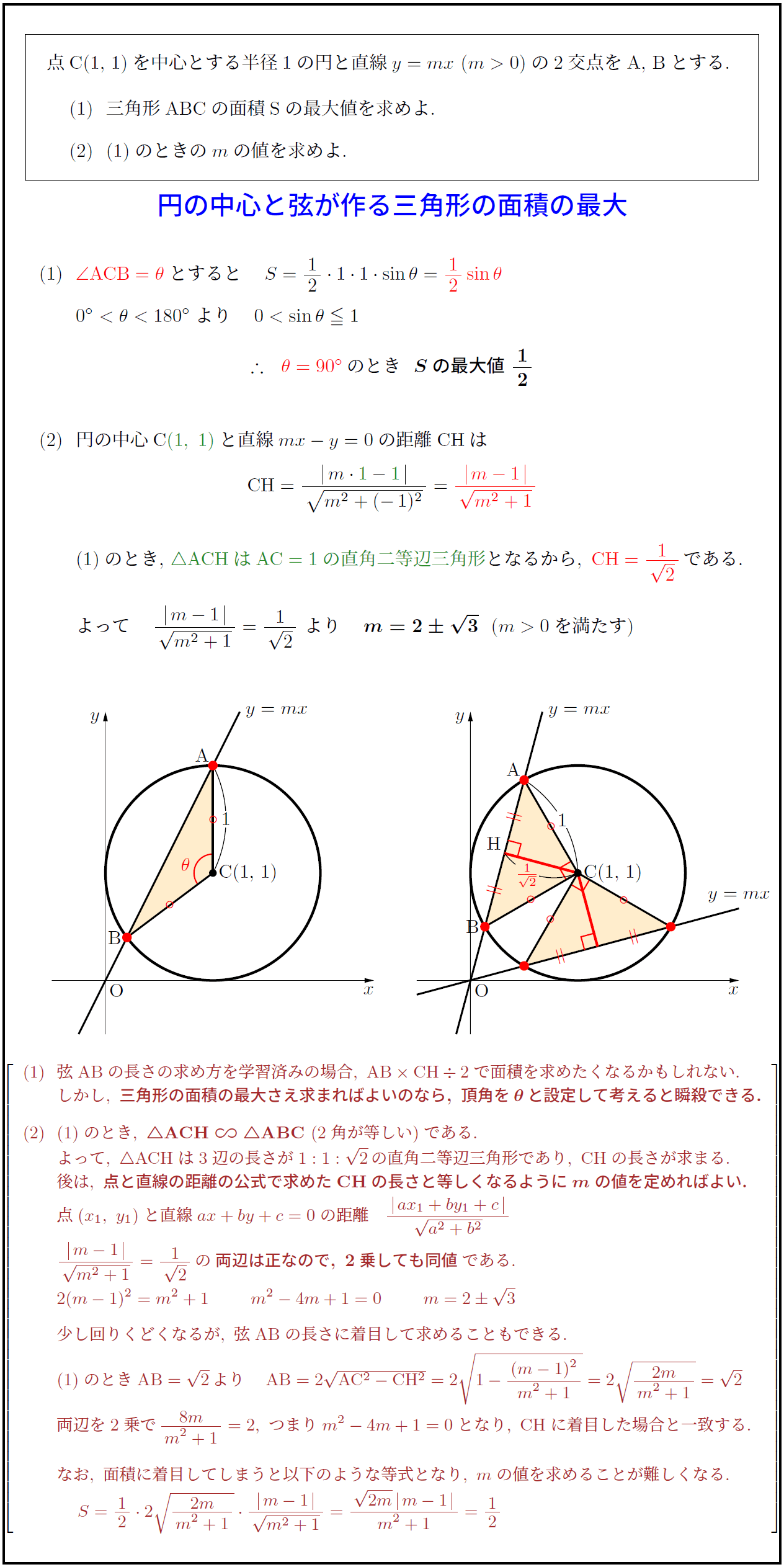



高校数学 円の中心と弦が作る三角形の面積の最大 受験の月




中学数学 3点を通る円の中心の書き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



1
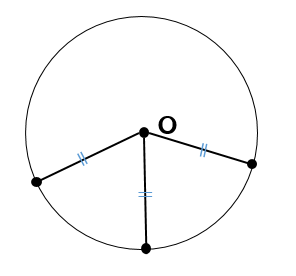



中1 作図 円の中心を求める方法を解説 数スタ
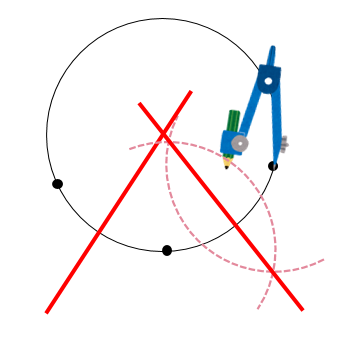



中1 作図 円の中心を求める方法を解説 数スタ



円周角と中心角 中学から数学だいすき



正三角形とは 定義や面積公式 高さや角度の求め方 受験辞典




円の方程式の求め方まとめ パターン別に解説するよ 数スタ




円 扇形 の面積 周や弧の長さの公式 数学fun
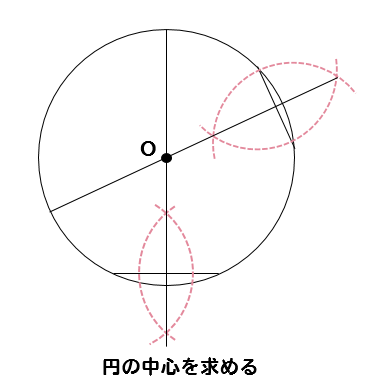



作図 円に内接する正三角形の作図方法とは 数スタ



扇形の中心角の求め方バウムクーヘンやドーナッツの様に 中心付近が無い扇形の中心 Yahoo 知恵袋




円の中心を求める 3つの方法 Wikihow



From灘 円の中心の求め方 朝日小学生新聞 中学受験eye 関西圏
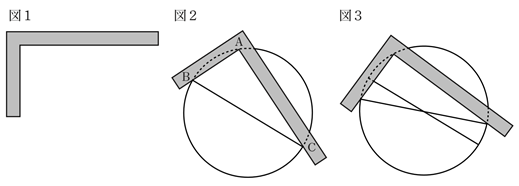



曲尺を使い円の中心を求める 1 準2級 カワズの数学ノート 数学検定 準2級




中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット




基本 2つの円の共有点 中心間の距離に注目 なかけんの数学ノート
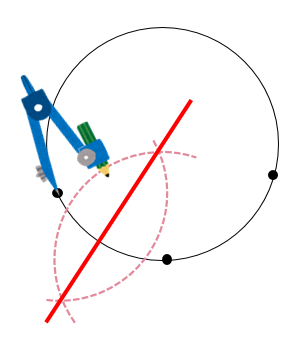



中1 作図 円の中心を求める方法を解説 数スタ
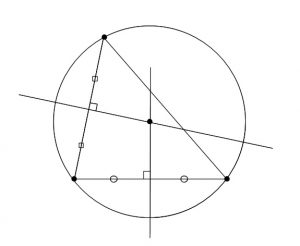



3点を通る円 と 2点とある直線上に中心がある円 の方程式の求め方




中学数学 円の中心の出し方 コンパス編 サクッとわかる なぜか分かる はかせちゃんの怪しい研究室




外心座標公式 基本 三角形の外心 Sed




中学数学 3点を通る円の中心の書き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



幾何計算 2点と半径から円の中心点を求めます Satoh




円周角の定理の証明 3つのパターンから分かる円周角と中心角の関係性 アタリマエ
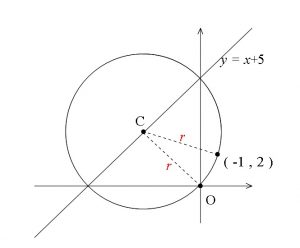



3点を通る円 と 2点とある直線上に中心がある円 の方程式の求め方




中心間の距離dの求め方を教えてください 数学aです よろしくお願いいたします Clear




おうぎ形の中心角の求め方 Youtube




1数 作図による円の中心の求め方 Youtube



Studydoctor円の公式と なぜ 中学1年数学 Studydoctor




3点を通る円を求める Qiita




作図 05 円の中心の求め方 Youtube




円の弧長 弦長 矢高 半径のどれか2つを与えて残りを計算 高精度計算サイト



円の中心の求め方 Love金沢水彩画
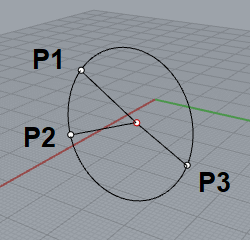



3次元空間での円の中心の求め方 Inak Engineering Llc



2 つの円の位置関係 思考力を鍛える数学
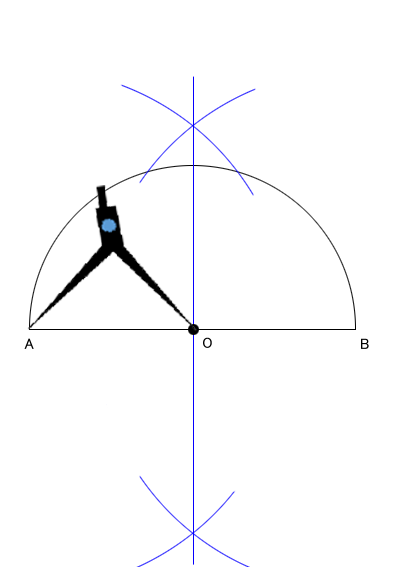



平面図形 おうぎ形 4 ネット塾




2つの点から円の方程式を求める 数学ii By Okボーイ マナペディア



円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典




円の中心を求める 3つの方法 Wikihow




外接円の半径の求め方がイラストで誰でも即わかる 練習問題付き 高校生向け受験応援メディア 受験のミカタ
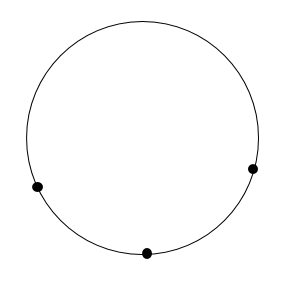



中1 作図 円の中心を求める方法を解説 数スタ
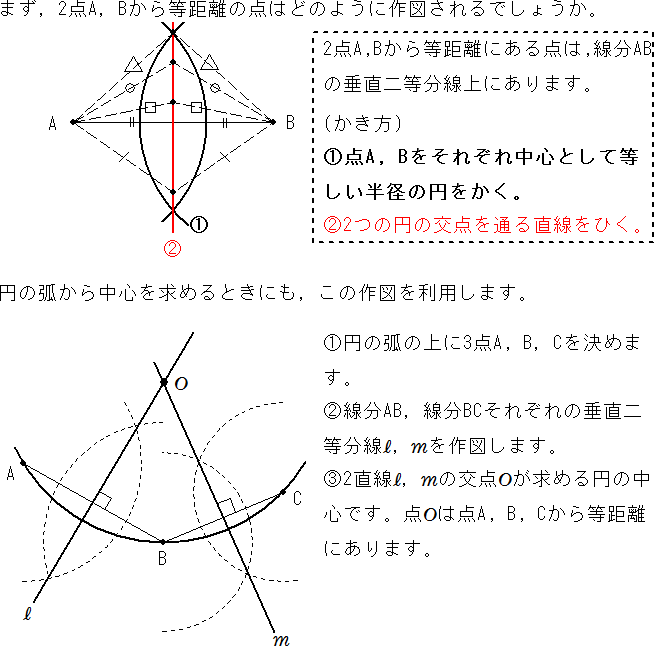



平面図形 円の中心を求める作図 中学数学 定期テスト対策サイト




垂直二等分線を使って円の中心をもとめる 中学数学 By Okボーイ マナペディア




平面図形 おうぎ形の中心角の求め方 中学数学 定期テスト対策サイト



家具製作資料 半径の判らない円弧半径の求め方 家具制作鯛工房



外接円 外心について



外接円とは 半径の公式や求め方 性質 書き方 受験辞典
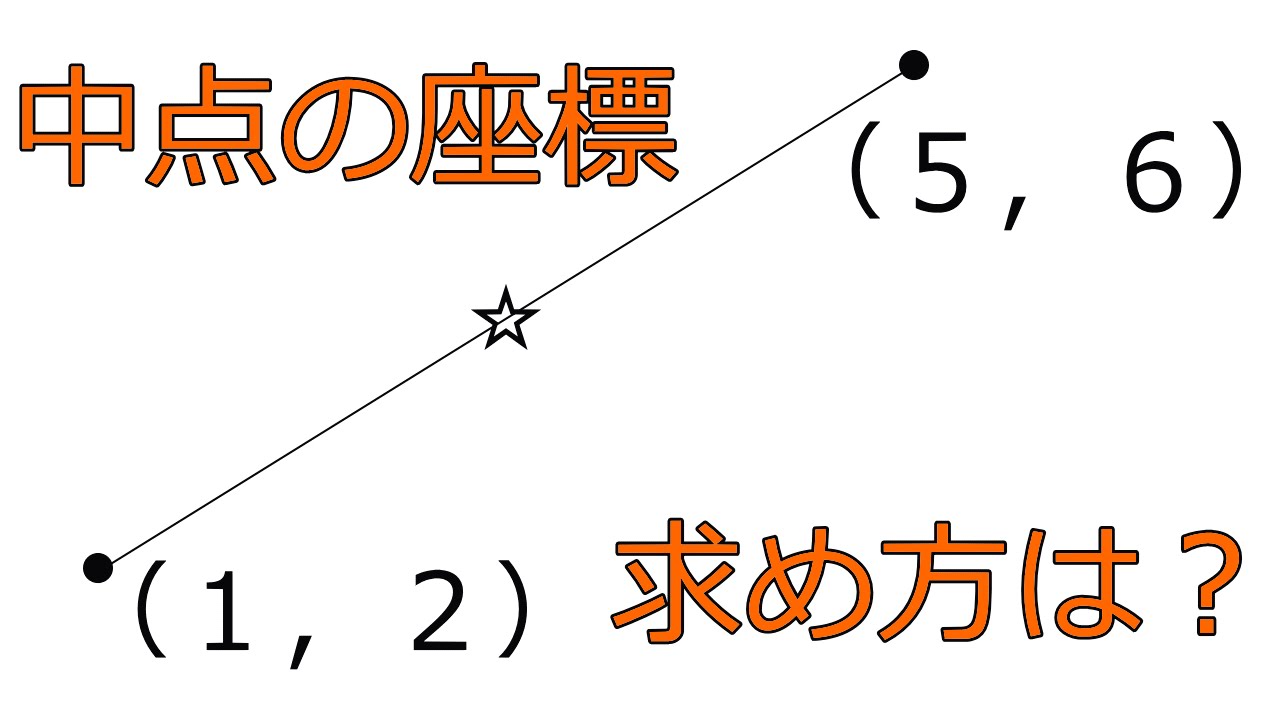



中点の座標の求め方 中学1年数学 Youtube




円の中心を求める 3つの方法 Wikihow




外接円の半径の求め方がイラストで誰でも即わかる 練習問題付き 高校生向け受験応援メディア 受験のミカタ



おう ぎ 形 の 面積 求め 方




三角形の外心について知っておきたい知識まとめ 理系ラボ



幾何計算 2点と半径から円の中心点を求めます Satoh




中学数学 円の中心の出し方 コンパス編 サクッとわかる なぜか分かる はかせちゃんの怪しい研究室




中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット
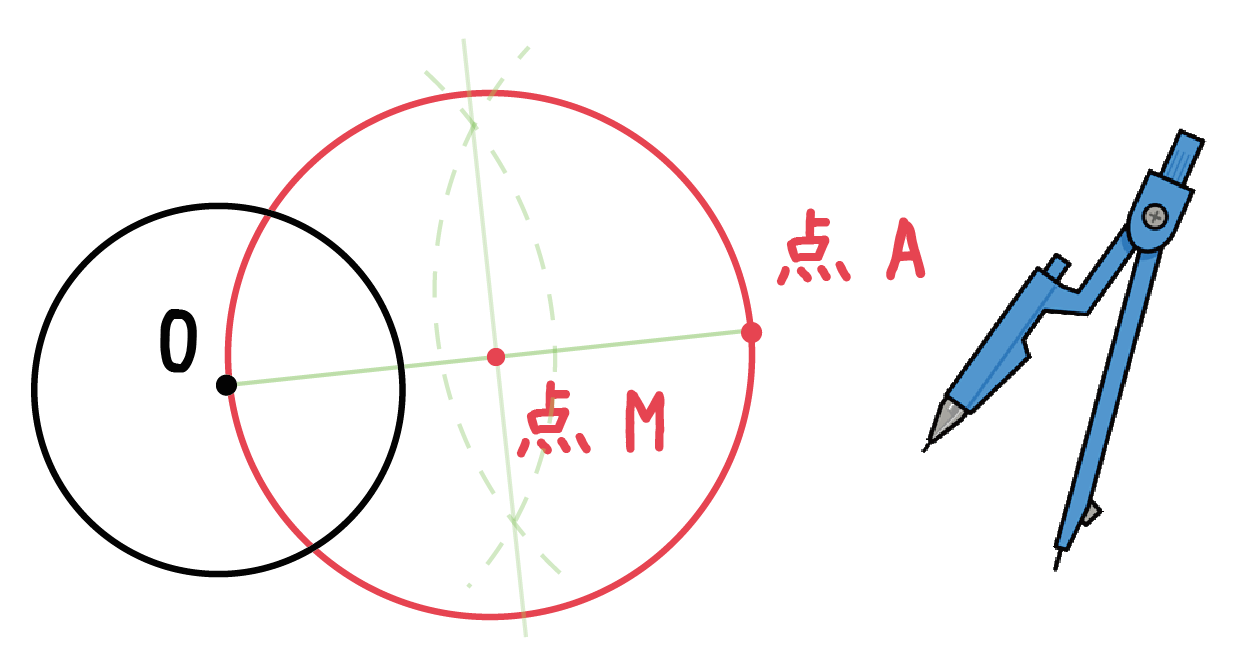



中学数学 円の接線をサクッと作図する2つの方法 Qikeru 学びを楽しくわかりやすく
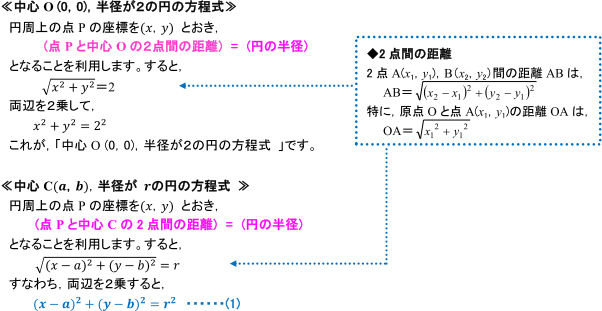



円の方程式の導き方 数学 苦手解決q A 進研ゼミ高校講座



3



外接円 外心について




円 半円 弧 扇形 の円周 面積の求め方と公式一覧 小学生の算数 Yattoke 小 中学生の学習サイト



1
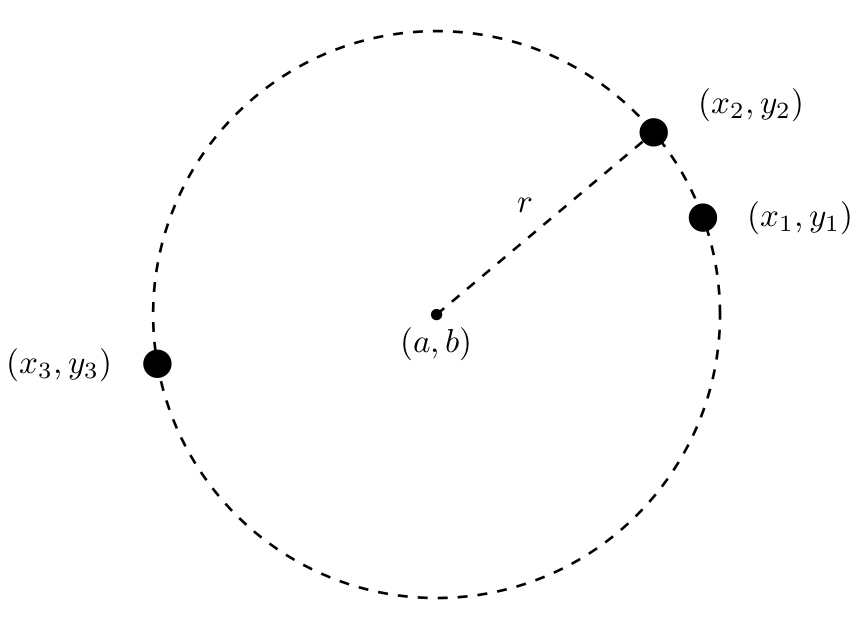



3点を通る円の中心と半径 Notes Jp




数学 円弧から円の中心が割り出せるのかを検証してみた 円弧のトレース用




円の中心の作図 コンパスを使って求める方法とは 中学数学 理科の学習まとめサイト



空き缶の中心の見つけ方 綿菓子を自宅で作ろう




数学 円すいの展開図 扇形の中心角は5秒で出せる 受験の秒殺テク 1 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




四角形の中心の求め方 四角形の中心 真中 の求め方は 各辺の真中を添付 Okwave




円の中心を求める 3つの方法 Wikihow




数学 円弧から円の中心が割り出せるのかを検証してみた 円弧のトレース用



幾何計算 2点と半径から円の中心点を求めます Satoh




中学数学 円の中心の出し方 コンパス編 サクッとわかる なぜか分かる はかせちゃんの怪しい研究室




円周角の定理と証明 中心角の求め方を詳しく解説 Rikeinvest




おうぎ形の弧の長さ 面積 中心角の求め方と公式 Irohabook




扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ




三角定規で円の中心を作図 おときち副塾長 電脳空間学習塾かもん Youtube
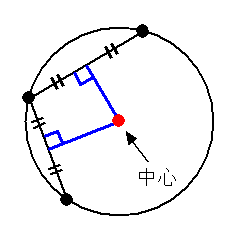



3次元空間での円の中心の求め方 Inak Engineering Llc




数学 円すいの展開図 扇形の中心角は5秒で出せる 受験の秒殺テク 1 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




円の中心の作図 コンパスを使って求める方法とは 中学数学 理科の学習まとめサイト
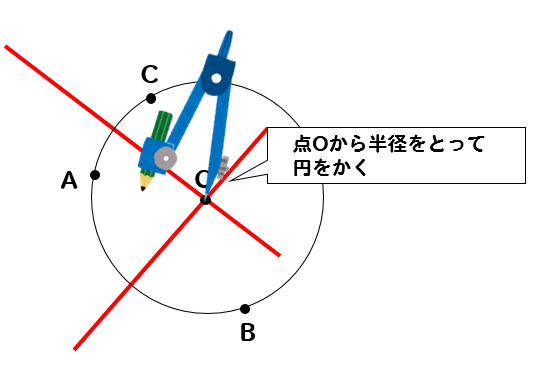



中1 作図 円の中心を求める方法を解説 数スタ




中3数学 円周角の定理 の3大重要ポイント 映像授業のtry It トライイット



1




垂直二等分線を使って円の中心をもとめる 中学数学 By Okボーイ マナペディア
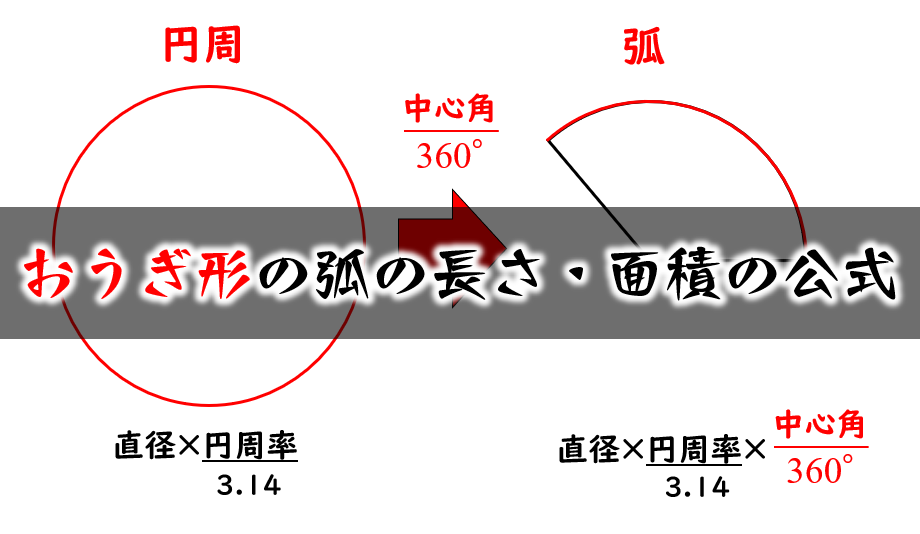



おうぎ形の弧の長さと面積の求め方 小学生に教えるための解説 数学fun




中3数学 円周角の定理 の3大重要ポイント 映像授業のtry It トライイット




カンタン公式 扇形の中心角の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




外接円の半径の求め方がイラストで誰でも即わかる 練習問題付き 高校生向け受験応援メディア 受験のミカタ




円の中心を求める 3つの方法 Wikihow



楕円の焦点の見つけ方 Geogebra




円の中心の出し方 コンパスなし 直径わからない編 シャンハイ山本弾工房



0 件のコメント:
コメントを投稿