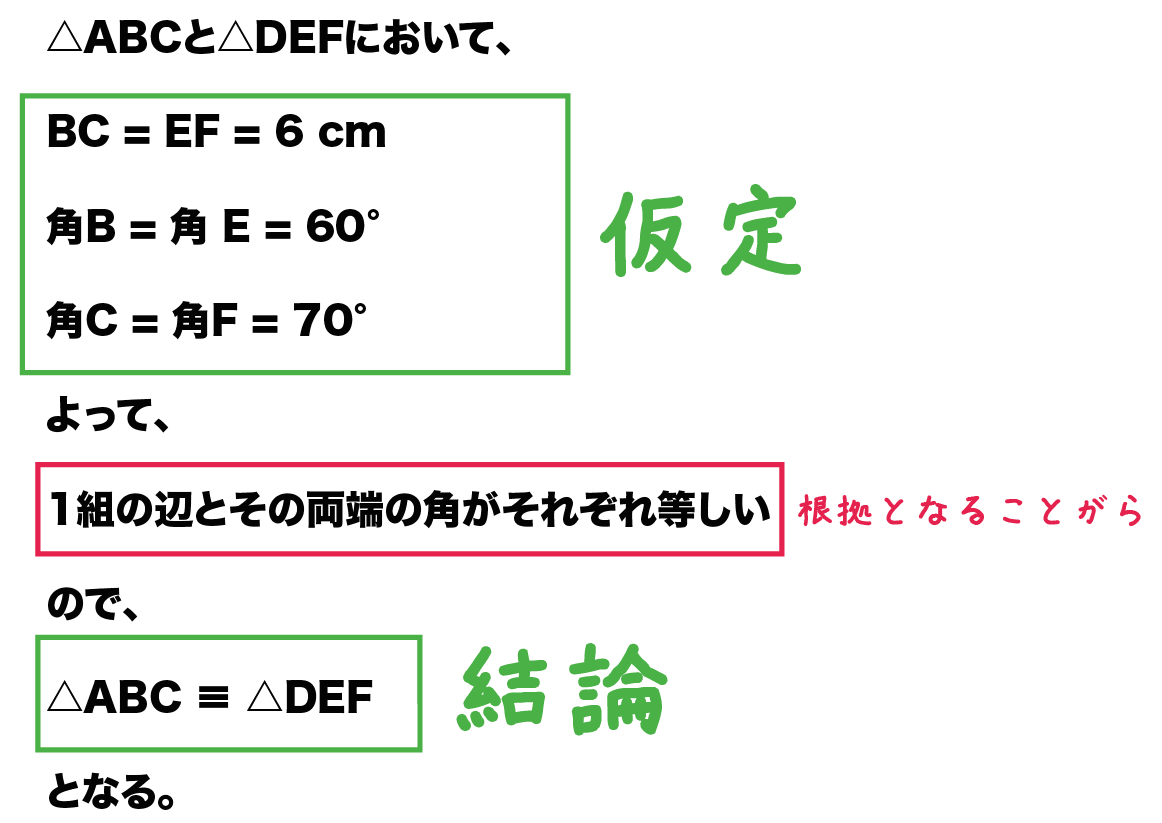
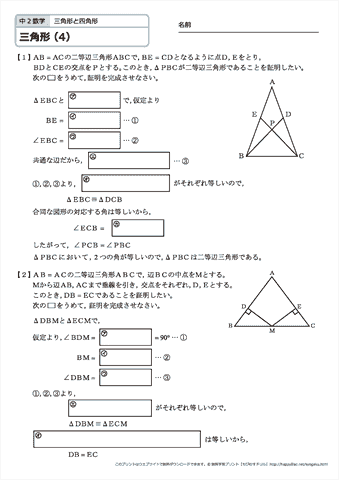
本研究では,数学教育における証明の意義 について考察し,それを基に中学3年生を対 象にした証明の意義理解調査を実施した。本 稿の目的は,この調査結果から生徒たちの証 明の意義理解の様相をよりよく把握し,証明明星大学 通信教育課程「pf3060 数学科教育法3 1単位目 19年度」の 合格レポートとなります。 なかなか合格できない方々に参考にして頂ければと思います。 1単位目 『中学2 年の「図形の性質と合同」の指導において、三角形の合同条件を利用して解く証明問題を2題考え、その解答と指導上の⑨ 根拠となることがらを明 確にして,図形の性質を考察 し,それを証明することがで きる。 ⑧ 簡単な命題について,その仮 定と結論を示すことができ る。 ⑨ 三角形の合同条件などを利 用した簡単な図形の性質の証 明について,根拠となることが

中2 数学 中2 5章 中学生 数学のノート Clear
中学二年 数学 証明 コツ
中学二年 数学 証明 コツ-19 年 2 月18 日 鈴 木 明 裕 (岐阜聖徳学園大学) 1.単元 図形の性質と証明 2.教材について h29 学習指導要領における位置づけ を考えると,b(2)図形の合同 (2)図形の合同について,数学的活動を通して,次の事項を身に付けることができるよ 3年数学 証明 3年数学 証明21曲一线五年高考三年模拟新教材版高中必修2第二册人教版高一下册5年高考3年模拟教材同步练习题册 共4本 高中数学物理化学生物 必修第二册21年考研数学三考试已结束,想查看21年考研数学三填空题真题答案、21年考研数学三选择题



数学の証明問題の解き方 セルモ大蔵 世田谷 の塾長ブログ
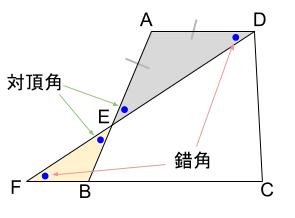
第3学年数学科指導案 日 時 平成25年10月22日(火)4校時 場 所 盛岡市立見前南中学校 3年1組教室 二つの図形が相似であることを読み取り,根拠を明らかにして説明していく。 相似条件を用いて証 明することができる。4 章 平行と合同 1 平行線と角,三角形と角 103 対頂角/同位角,錯角/平行線と角/長 方形の折り返し/平行線になるための条明は1368年に漢民族によって建国された。国内の混乱などでおとろえていた元は北へ追いやられた。 明は伝統的な朝貢貿易をおこなった。 二度の世界大戦 中学校数学学習サイト 中学数学
版二年级数学下册综合练习题docx,版二年级数学下册综合练习题 版二年级数学下册综合练习题 PAGE PAGE / NUMPAGESPAGE25 版二年级数学下册综合练习题 PAGE 小学二年级下综合练习题 dou 小学二年级数学下册综合练习题(一) 一、口算 380-0= 28÷4= 43+50= 6×7= 87-55= 51÷7= 37+45= 71-26= 1600-700= 5900-00= 74数学navi テキスト 中学2年 第6章 定理と証明 テキストの使用方法 このテキストは「数学ナビ」の学習をすすめるためのテキストです。ですから、「数学ナビ」 を使用して学習する際に有効的に使用して1年の復習 4 1 章 式の計算 1 式の計算⑴ 13 単項式と多項式/同類項をまとめる/加 法・減法/数と多項式の乗法・除法/分 配
中学数学通信 13年 秋号 b二つの事物があって,a,bともに性質 には縁遠いように思われがちであるが,証 明に限らず,以下の例にみられるように,前ちゃんの中学校数学の部屋:パワーポイント補助教材2年 教材のダウンロード プレゼンテーション教材 2年 この教材を使用した授業方法は、 こちら をご参考にしてください。 ダウンロードに関する 注意事項 ダウンロードの前にお読みください2年生 5 図形の性質と証明 数学的な思考力・判断力・表現力をはぐくむ問題 年 組 号氏名 全国学力・学習状況調査 B問題① 1 下の図のように,線分ABの垂直二等分線ℓをひいて,線分ABとの交点をMとします。また,直 線3ℓ3上に点Pをとります。h19



中学2年数学証明について 写真にある証明文は模範解答と違 Yahoo 知恵袋




中学2年数学 証明って難しいよ あき先生のフォローアップ授業
岐阜数学教育研究 05, Vol4, 16 2倍取りゲームの数理を扱った授業の提案 冨倉亮1, 石渡哲哉2 本報告書では平成16年10月24日に,中学校三年生から高校二年生までを対象に行っ た授業について報告する。2年 数学1 第2学年数学科学習指導案 日 時 平成28年11月9日(水)5校時 1400~1450 学 級 花巻市立花巻中学校2年3組 計32名 (男子16名 女子16名) 指導者 教諭 土谷 雄介 1 単元名 4章 平行と合同 2 単元について (1) 教材について接線と弦のつくる角の定理の証明 では、なぜこのような定理が成り立つのか。 簡単に確認しておきましょう! なぜ、次のような位置にある角の大きさが等しくなるのでしょうか。 これを考えるには、まず 接点から、直径になるように線を引いて 下の




中2 数学 中2 5章 中学生 数学のノート Clear




中2数学 証明とは 練習編 映像授業のtry It トライイット
「初 解きフェス参加🐣💓 ところどころをタップしてみれば、答えが見れます。 ぜひ解いてみてください笑 (かなり簡単です🍀)」, 学年 中学2年生, キーワード 解きフェス,なる'sノート二年数学下:《第四单元-表内除法(二) 整理和复习(二)》设计 第九课时 整理和复习(二)教学内容:课本p63页第2题,练习十四第7~10题 教学目标:1、让学生会综合应用所学知识解决简单的或稍复杂的实际问题,在解决问题的过程中使学生学会转化的数学方法。昭和37年 新しい数学 2 昭和56年 新しい数学 2 平成28年 新しい数学 2 図形の性質と証明 6-3-3制の学校教育制度が始まり,義務教育が9 年間に延長された昭和年代の中学校数学では「証 明」という用語は使われていませんでした。当時の学




無料 中2数学 発展問題 解答プリント 228 三角形 四角形1 二等辺三角形




無料 中2数学 標準問題 解答プリント 227 図形7 復習
2年生 5 図形の性質と証明 知識・技能の習得を図る問題 年 組 号 氏名 全国学力・学習状況調査 A問題 ③ 3 下の図のようなAB=ACの二等辺三角形ABCがあります。辺AB,辺AC上にBD=CEとなる 点D,点Eをそれぞれとります。中学3年 数学 目標 隣あう2つの偶数の積に1をたした数の性質を見つけ,それを証明することを通して,展開や因数分解を利用 した証明の仕方を理解し,結果から類推的に考えて性質を見つけ,それを文字式の計算を利用して証明できる 这就证明了二项式定理 方法(二)数学归纳法 当然成立 假设 时定理成立,即 则 时 根据之后会讲到的组合恒等式 这样便由数学归纳法证明了二项式定理 二项式系数的性质 (1)对称性 证明: 方法(一) 直接由定义 方法(二)余弦定理 b2=a2c22accosB 注:角B是边a和边



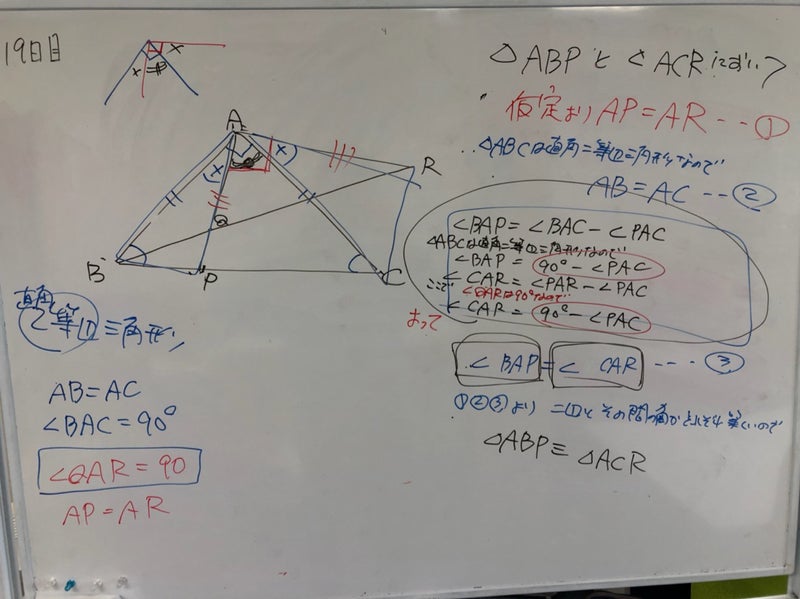
平成25年長野県立高校 入試問題 図形の証明問題 合同 現役塾講師のわかりやすい中学数学の解き方




中2数学 証明のしくみ 大日本図書 赤城 ᐡᐤᐡ
論理的な図形認識を促す算数・数学科カリキュラム開発(4) すること」があげられており,証明を書くだけでなく証 明を読むことの大切さを述べている。 の性質と証明」で,二等辺三角形の性質2年1組 数学科学習指導案 平成25年10月28日(月) 3校時 明することを目的として個々の生徒が積極的に考えるようにしたい。 証11証明の意味と必要性 ・証明の意味と必要性、仮定、結論、証明のすじ道について理Share your videos with friends, family, and the world



Studydoctor作図の証明 中2数学 Studydoctor




世界一わかりやすい数学問題集中2 5章 図形の性質と証明
上越数学教育研究,第21号,上越教育大学数学教室,06年,pp8194 中学校数学における証明の正当化に関する研究 灰野 仁 上越教育大学大学院修士課程2年 1.はじめに 文部省(1999)は,図形指導の意義として図 形の概念形成と性質の理解及び,論理的な思 考一級建築士 二級建築士 ・英文成績証明書 ・ 学力に関する証明書 (教職関係) 英文証明書の種類1通2,000円 ・英文卒業証明書 ・卒業証明書 ・ 成績証明書 ( 中学・技術 中学・数学 証 明 書 申 込 書3 年数学 1 第3学年 数学科学習指導案 日時 平成26 年11 月14 日(金)2校時 について学習し,二つの図形の形が同じであるということを縮図や拡大図を通して理解していきて の相似条件を用いて証 明することができる。 7 ③相似の 利用




これで点が取れる 単元末テスト中2数学 4章 平行と合同と証明




中2 数学 中2 証明 中学生 数学のノート Clear
本単元は,中学校学習指導要領解説数学編第3学年「B 図形 」の内容に,「図形の性質を三角形の 図について学習しており,二つの図形の形がじであるということを縮図や拡大図を通して理解して また,図形の性質を証 明することができる。 ②日常のFdData 中間期末:中学数学2 年:四角形 平行四辺形の性質/平行四辺形についての計算問題/平行四辺形の性質:三角形の合同/ 二等辺三角形・正三角形など /平行四辺形になる条件/平行四辺形になることの証明/ 対角線に注目/ 二年级数学测试题打印版——推荐doc,word文档可编辑——欢迎下载 word文档可编辑——欢迎下载 word文档可编辑——欢迎下载 二年级数学第一单元测试题 口算: 5×8= 6×4= 7×3= 5×6= 4×8= 5×2= 2×3= 9×7= 9×6= 2×8= 5×4= 6×7= 4×3= 3×6= 7×5= 下是张老师调查本班同学最喜欢的业余生活情况统计表 活动项目 看书




中2 中2 数学 5章 図形の性質と証明 プレイカラー 中学生 数学のノート Clear



無料 中2数学 応用 発展問題 問題プリント 327 図形の相似2 相似条件と証明
公開日時 16年11月27日 16時33分 更新日時 16年11月27日 19時44分 16年11月27日 19時44分− b ± b 2 − 4 a c 2 a \dfrac{b\pm\sqrt{b^24ac}}{2a} 2 a − b ± b 2 − 4 a c は確かに二次方程式の解である(以下のように代入によって簡単に確認できる)。 年dmm中国站比赛信息已经公布 (1)时间拟定年8月6日9日,4天; (2)地点拟定江苏昆山; 比赛项目等与往年相同,详情见下面微信推文: dmm 错过了amc,可别再错过杜克大学青少年数学大会! 一、活21年北京市中学生数学竞赛初赛_高一试题 答案和解析 高中数开学考试月考单元




平行四辺形の証明問題 無料で使える中学学習プリント




数学 中2 60 証明のしくみ Youtube
数学科学習指導案 指導者 後 藤 春 香 日日日日 時時時時 平成24年12月1日(土) 第1校時(10:00~10:50) 年年年年 組組組組 中学校第2学年2組 計39名(男子19名,女子名) 場場場場 所所所所 中学校第2学年2組教室 証明問題「√3 が無理数であることを証明」 有理数・無理数とは? 定義 有理数とは、 整数のわり算、つまり分数で表せる実数 です。 整数 整数( 整数 整数 )にできる数すべてをいいます。 一方、無理数とは 有理数ではないそのほかの実数 です。




中2数学 二等辺三角形の性質2 頂角の二等分線 練習編 映像授業のtry It トライイット



中学2年の数学 動画 証明のしくみの問題 19ch



3
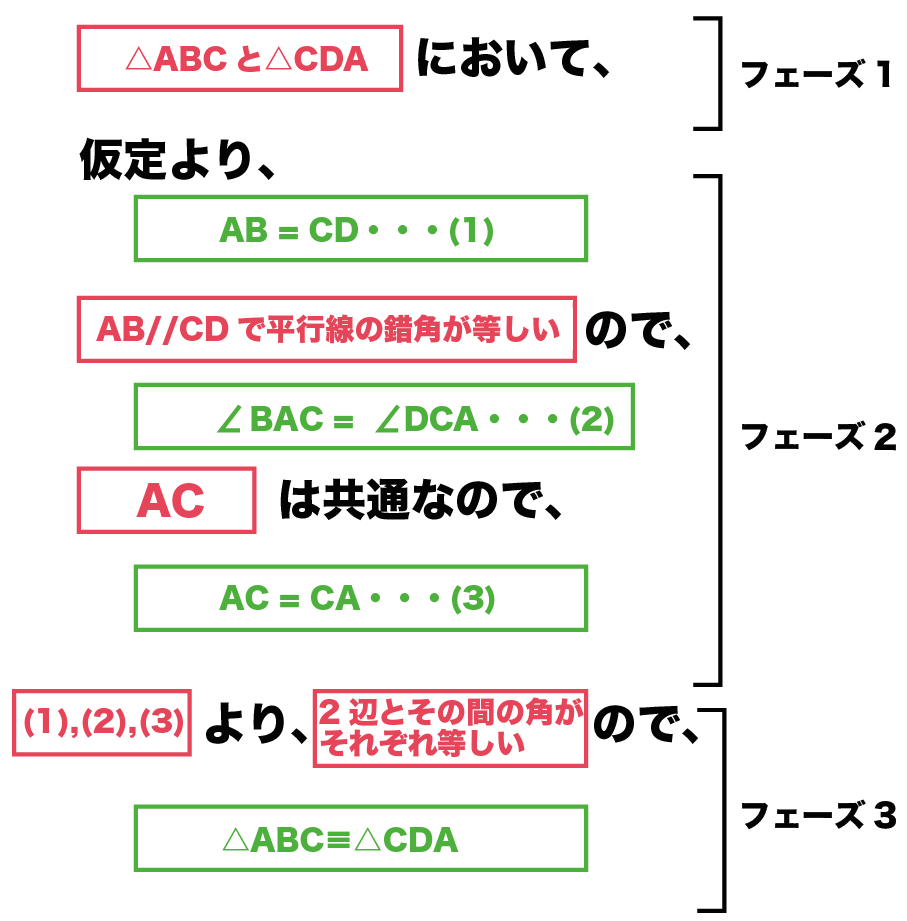



中学数学 3年間つかえる証明問題の書き方 Qikeru 学びを楽しくわかりやすく




世界一わかりやすい数学問題集中2 5章 図形の性質と証明
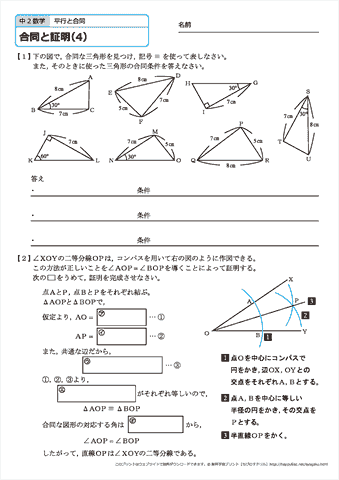



中学2年生 数学 合同と証明 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




この様な中学二年生で習う 応用問題である証明問題での質問です この証明問題は Clear
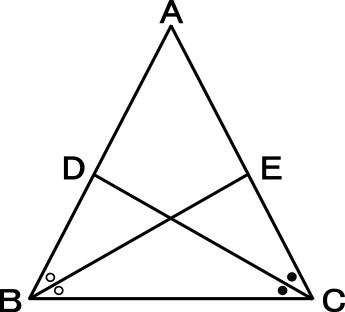



中学2年数学練習問題 図形と合同 三角形の合同の証明問題



1



中学2年の数学証明の問題を解いてください お願いします Yahoo 知恵袋




中学2年 数学 証明まとめ 中学生 数学のノート Clear
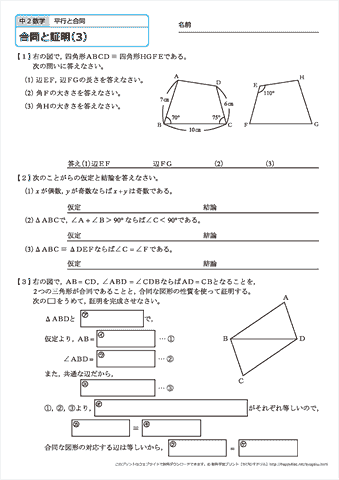



中学2年生 数学 合同と証明 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




無料 中2数学 基本問題 解答プリント 228 三角形 四角形1 二等辺三角形
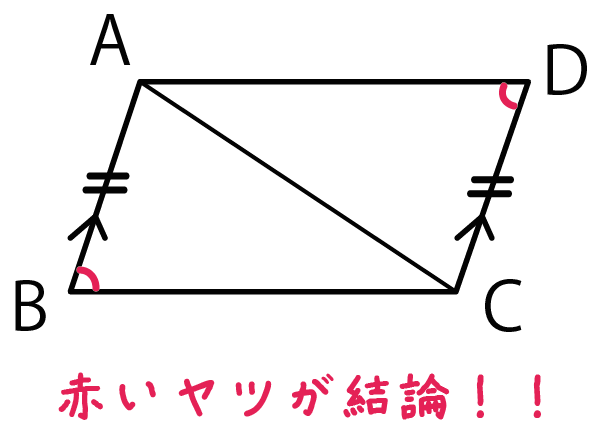



中2数学 図形の証明問題を攻略できる7つのコツ Qikeru 学びを楽しくわかりやすく




三角形の合同条件を使った証明問題 中学2年生の問題を解こう 身勝手な主張




世界一わかりやすい数学問題集中2 5章 図形の性質と証明




中学校2年生の数学の授業




無料 中2数学 テスト対策 解答プリント 216 図形と合同4 平行四辺形




数学の証明問題の解き方 セルモ大蔵 世田谷 の塾長ブログ




誰でもわかる 数学 中学2年 証明 Youtube




中2数学 三角形の合同の証明の解き方の手順 こいがくぼ翼学習塾




単純閉曲面に囲まれた図形の重心1 中学3年生数学教科書からの三角形の重心についての証明問題 身勝手な主張
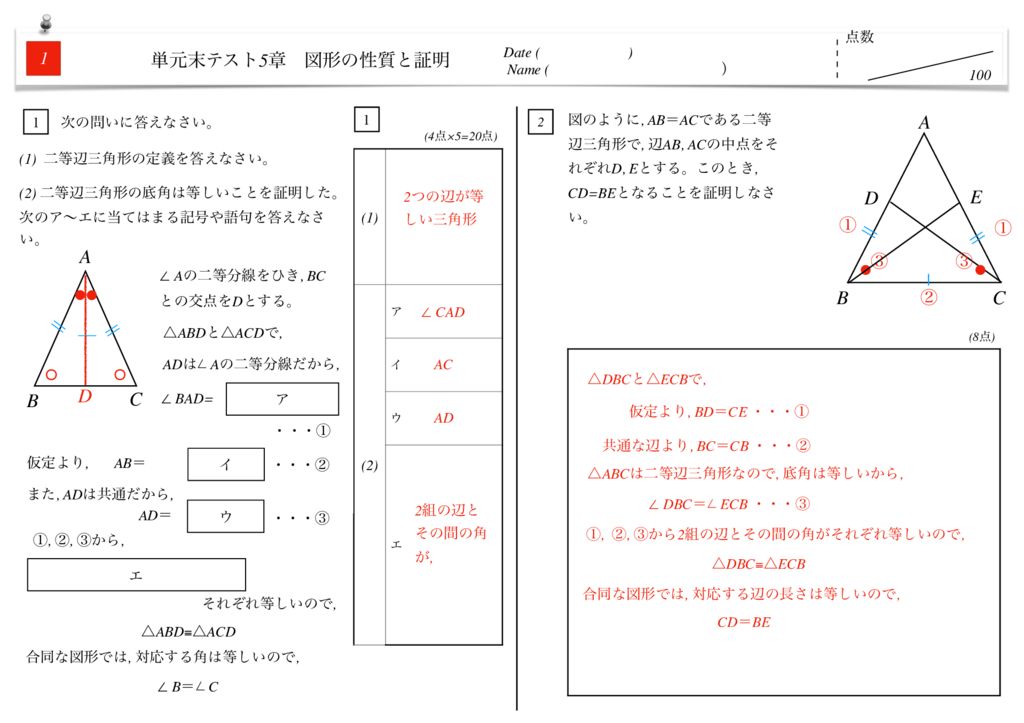



これで点が取れる 単元末テスト中2数学 5章 図形の性質と証明
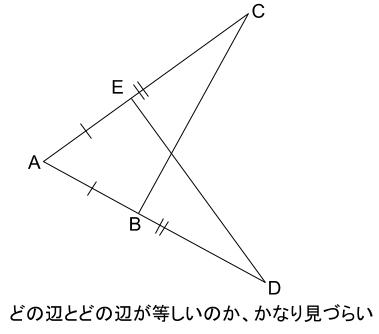



中学数学 三角形の合同の証明 その2 中学数学の無料オンライン学習サイトchu Su
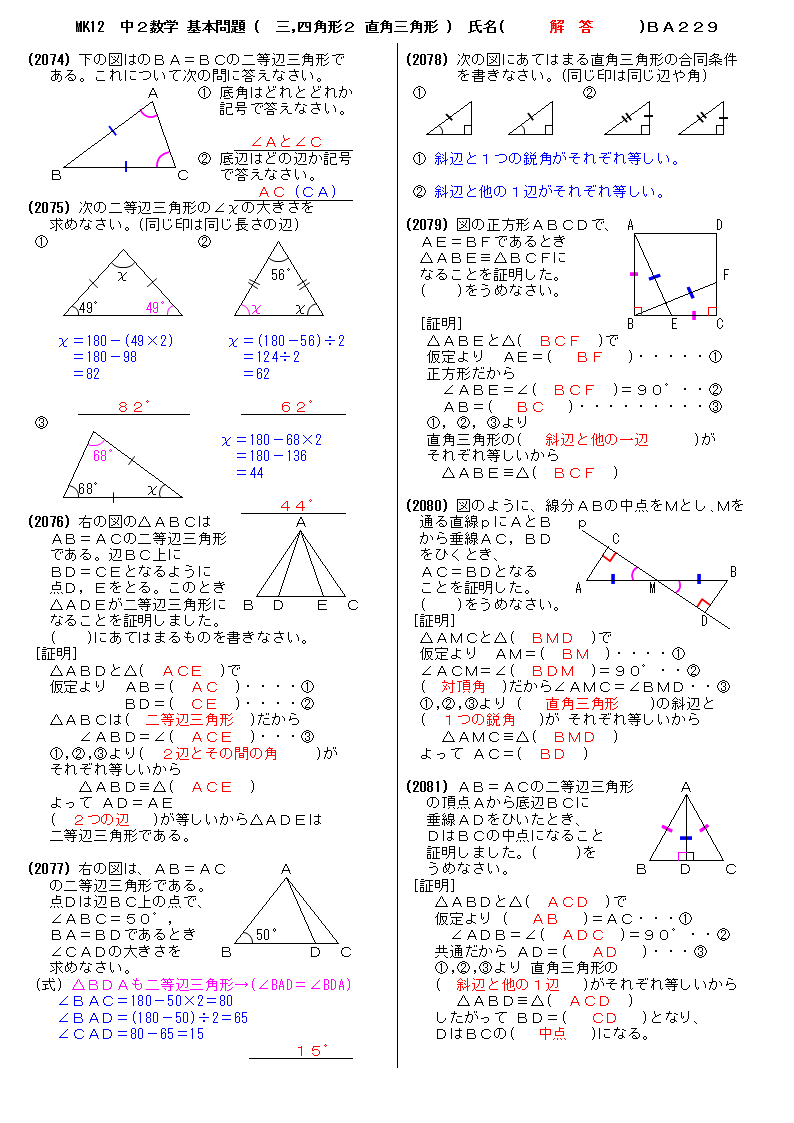



無料 中2数学 基本問題 解答プリント 229 三角形 四角形2 直角三角形
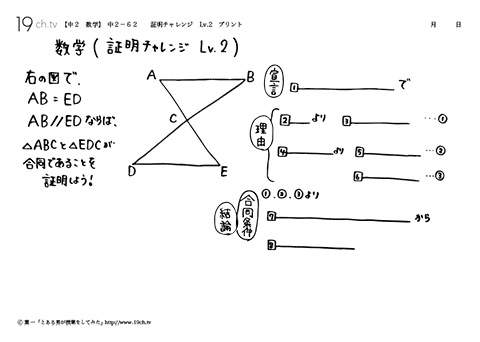



中学2年の数学 動画 証明チャレンジ Lv 2の問題 19ch
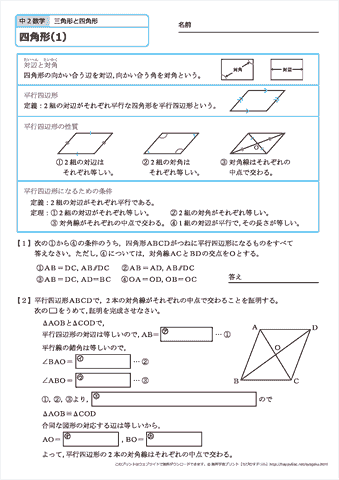



中学2年生 数学 四角形 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
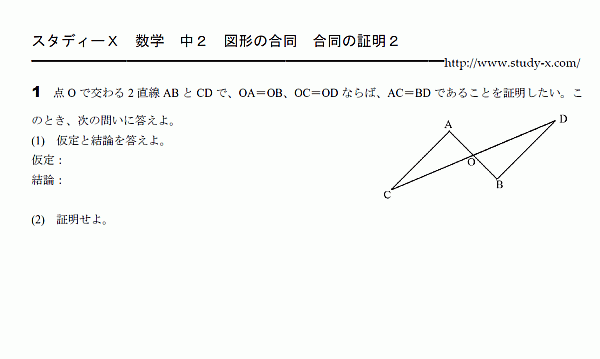



中2 数学 無料学習プリント教材



Studydoctor三角形の合同の証明 応用 中2数学 Studydoctor




中学2年生 数学 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




苦手な人が多い図形の証明問題を解くコツを解説 実は非常に簡単なんです 学習塾 Step By Step




いえがくサポート 勉強が超 苦手な中学生の勉強方法 中2数学



Math 角度の難問 中学2年生 働きアリ




中2数学 三角形の合同の証明の流れ 3学期期末テスト用 赤城 ᐡᐤᐡ



中学2年数学証明 この問題の証明を教えてください Yahoo 知恵袋



中学2年数学証明の問題です 解いてみたのですが 模範解答と違って Yahoo 知恵袋




中2 数学 中2 5章 中学生 数学のノート Clear



中2数学 証明とはいったいなにもの Qikeru 学びを楽しくわかりやすく



中2数学 図形の証明問題を攻略できる7つのコツ Qikeru 学びを楽しくわかりやすく



数学 中学証明問題を解く4つのポイント




図形に関する性質の証明 身勝手な主張



中学2年生 数学 合同と証明 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



Q Tbn And9gcs8jzs Zkdiyrmuisoi0mwqzez E9r9gwygbti5ixce9rlyfs0 Usqp Cau
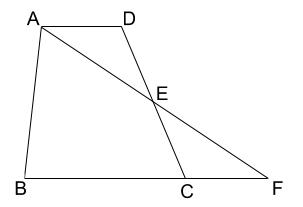



中学数学 三角形の合同の証明の利用 その1 中学数学の無料オンライン学習サイトchu Su



中2数学 学年末テストの証明問題よく出るパターンをまとめてみた 個別指導塾のyou 学舎日記 公式ブログ
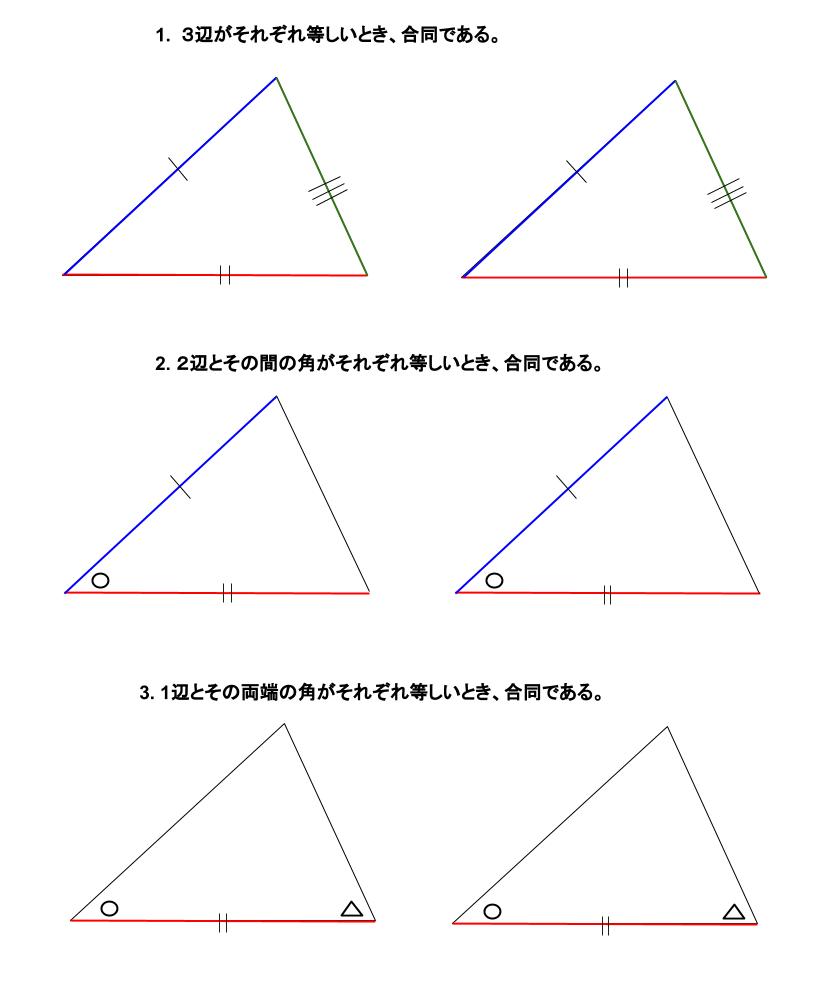



中学数学 三角形の合同条件 中学数学の無料オンライン学習サイトchu Su




無料 中2数学 基本解説 問題プリント 226 図形6 証明のしくみと根拠



中学2年生 数学 三角形 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



中2数学 発展問題プリント12 図形6 証明のしくみと根拠 問題 226
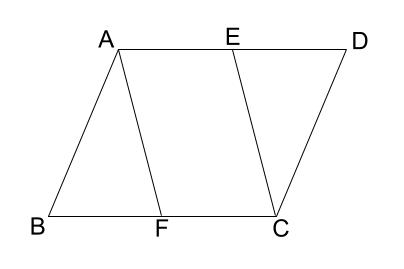



中学数学 証明 平行四辺形の性質の利用 中学数学の無料オンライン学習サイトchu Su




無料 中2数学 基本問題 解答プリント 226 図形6 証明のしくみと根拠
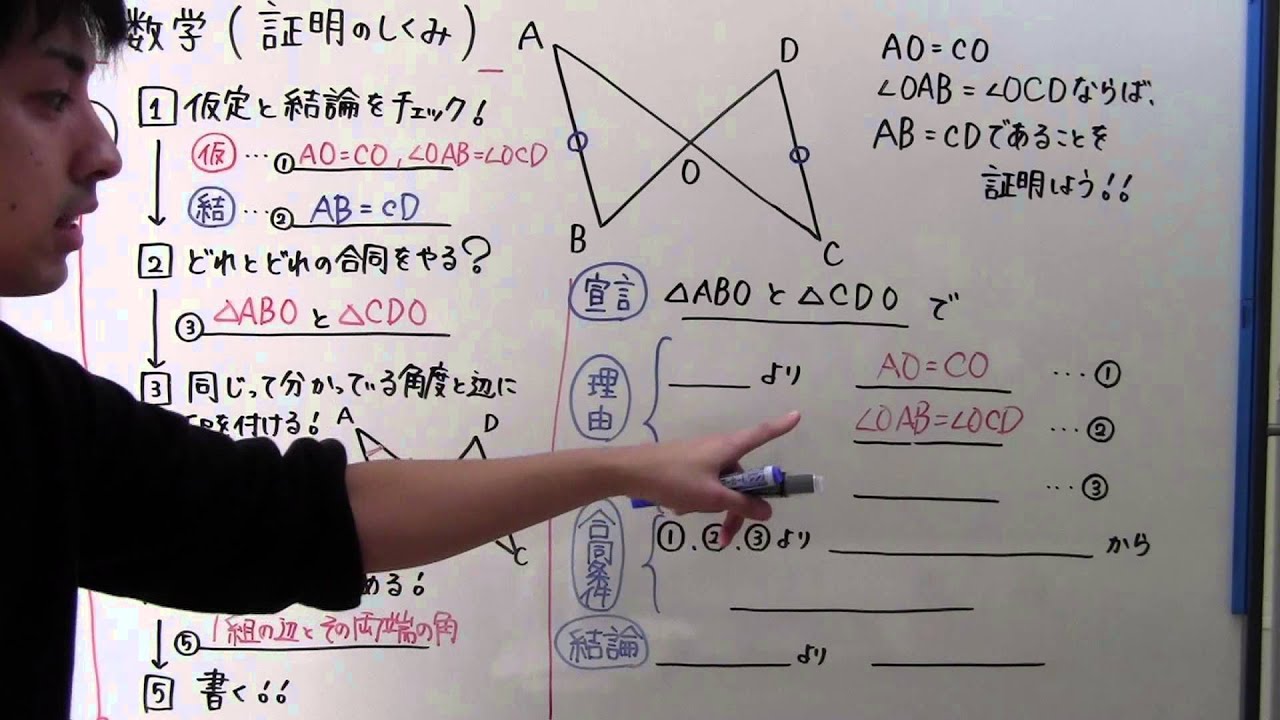



中2 数学 中2 60 証明のしくみ Youtube
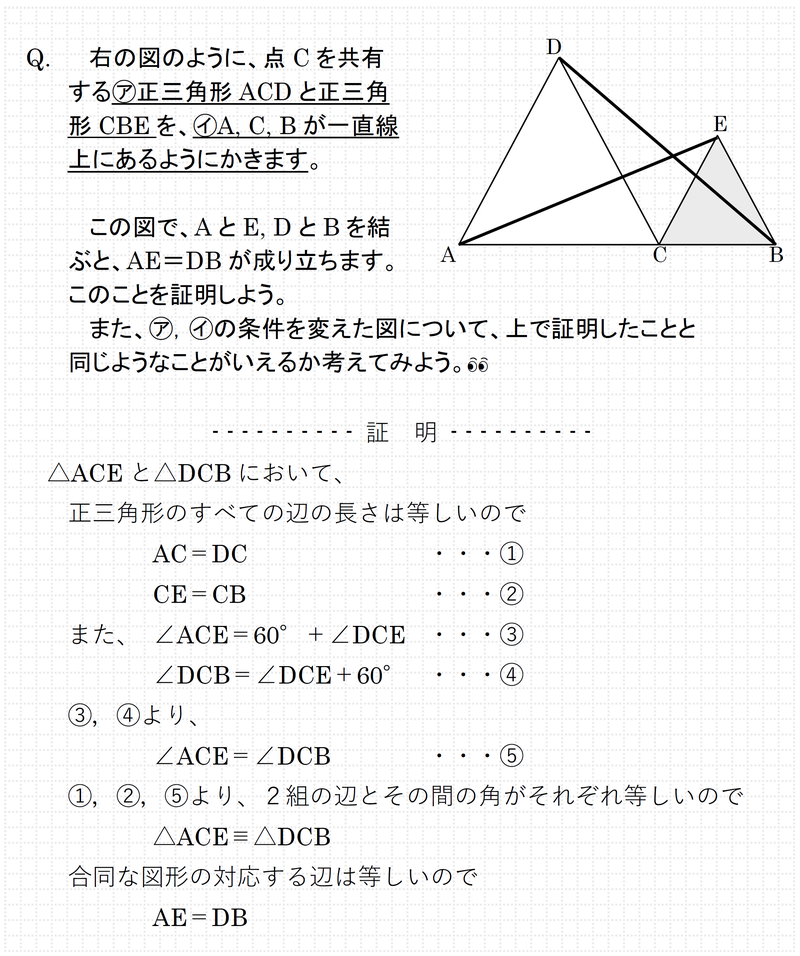



70以上 中学 数学 証明 問題 ニスヌーピー 壁紙




中学数学より3 三角形の合同条件 身勝手な主張




角度の問題まとめ 無料で使える中学学習プリント




中学2年数学練習問題 図形の合同と証明の定期テスト対策問題
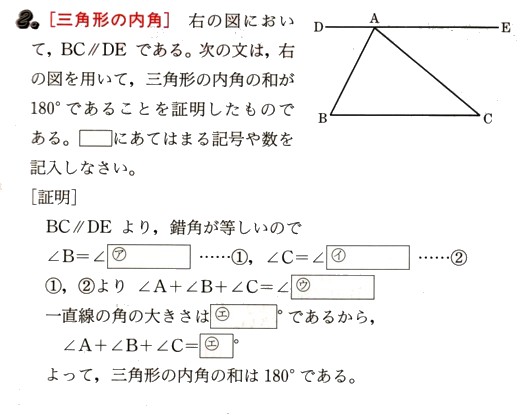



中学2年数学 図形の調べ方 図形と証明 練習問題2 あんのん塾



Q Tbn And9gcq0ni0zzk0oudu Jh Q6ecx2ihdqj1rql3yb4afti Kz7awmd8q Usqp Cau
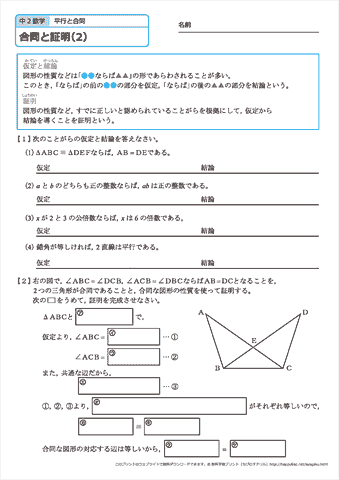



中学2年生 数学 合同と証明 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
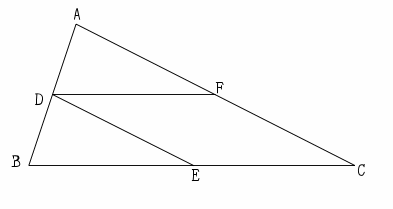



合同の証明2




中学2年 数学 証明の解き方 教えてください 証明が まったく わかり 数学 教えて Goo
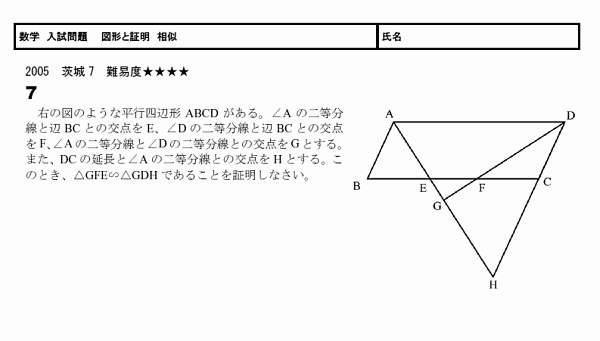



中学 数学 問題 無料学習プリント教材
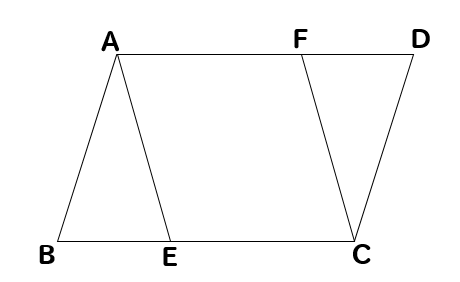



中学数学 平行四辺形の証明問題を徹底解説 数スタ
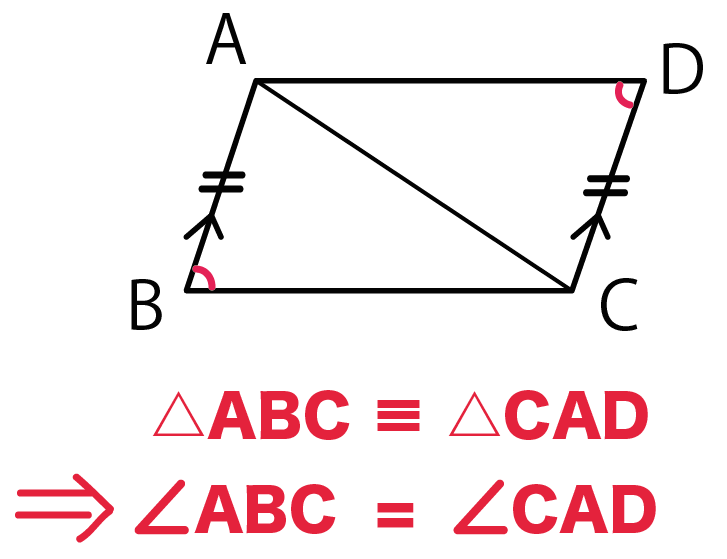



中2数学 図形の証明問題を攻略できる7つのコツ Qikeru 学びを楽しくわかりやすく
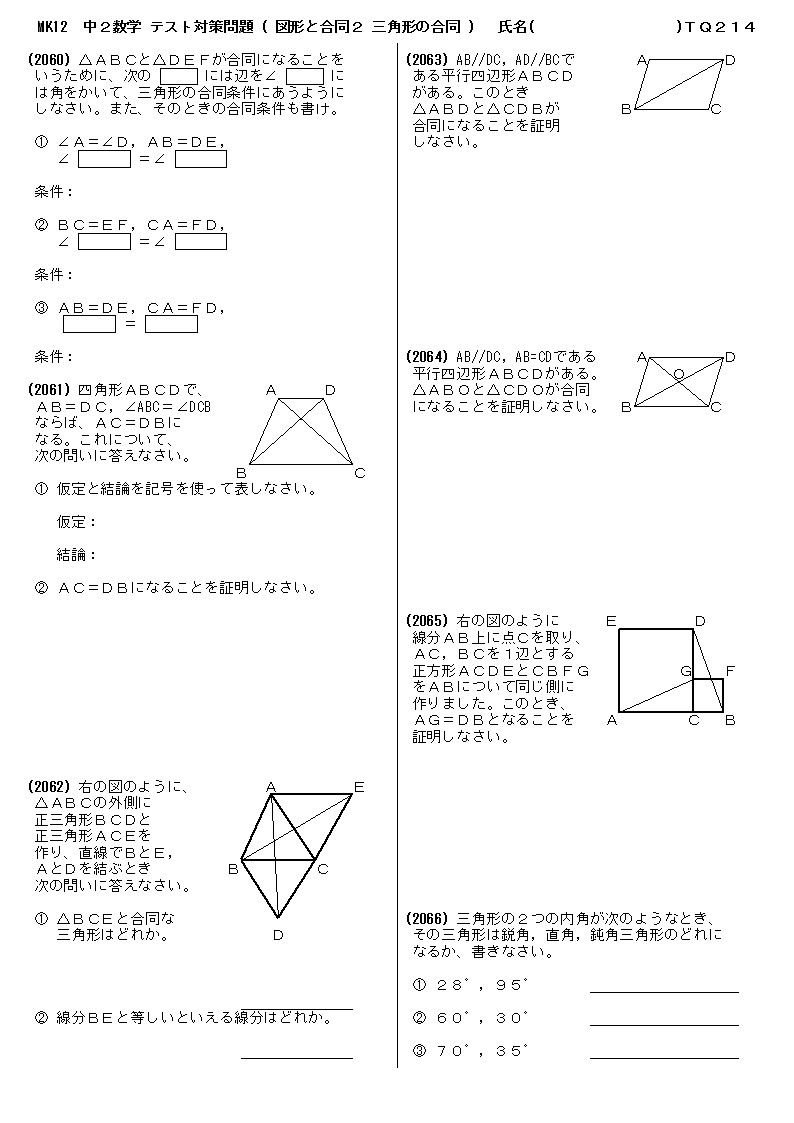



無料 中2数学 テスト対策 問題プリント 214 図形と合同2 三角形の合同




数学2年 文字式の利用 塾の先生が作った本当に欲しいプリント 楽天ブログ




超 パワーアップ中学数学 図形の証明 中継点 文字式の表現 活用テクニック Myisbn デザインエッグ社 長通 幸大 本 通販 Amazon




中学2年数学練習問題 図形の合同証明の復習と定期テスト対策問題




世界一わかりやすい数学問題集中2 4章 平行と合同と証明
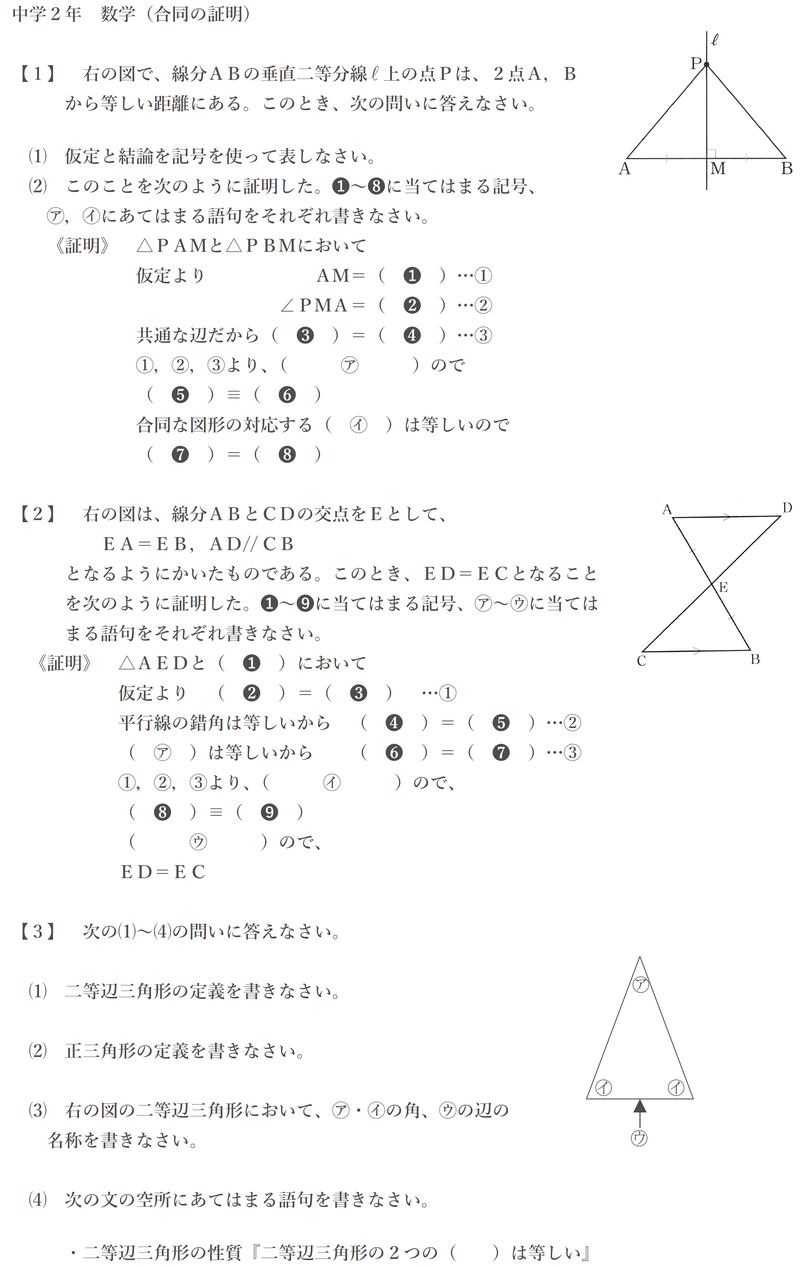



中2数学 三角形の合同の証明の流れ 3学期期末テスト用 赤城 ᐡᐤᐡ



中2数学 学年末テストの証明問題よく出るパターンをまとめてみた 個別指導塾のyou 学舎日記 公式ブログ
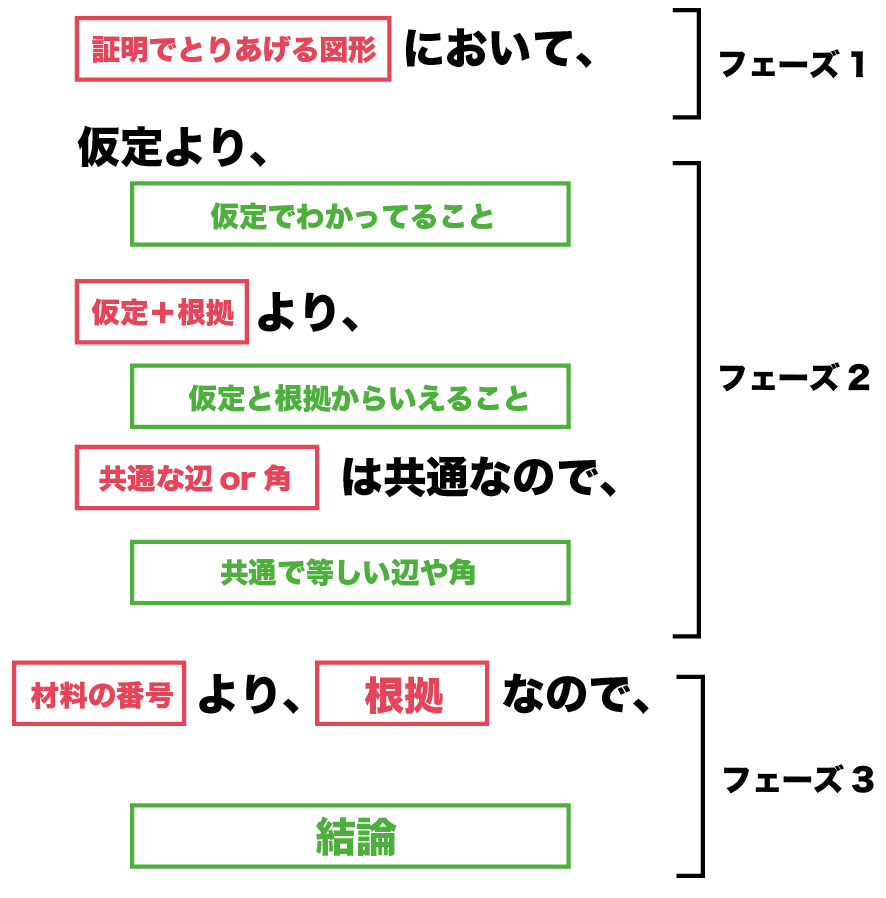



中学数学 3年間つかえる証明問題の書き方 Qikeru 学びを楽しくわかりやすく




中2数学 証明とは 例題編 映像授業のtry It トライイット




平行四辺形の証明問題 無料で使える中学学習プリント




無料 中2数学 標準問題 解答プリント 228 三角形 四角形1 二等辺三角形
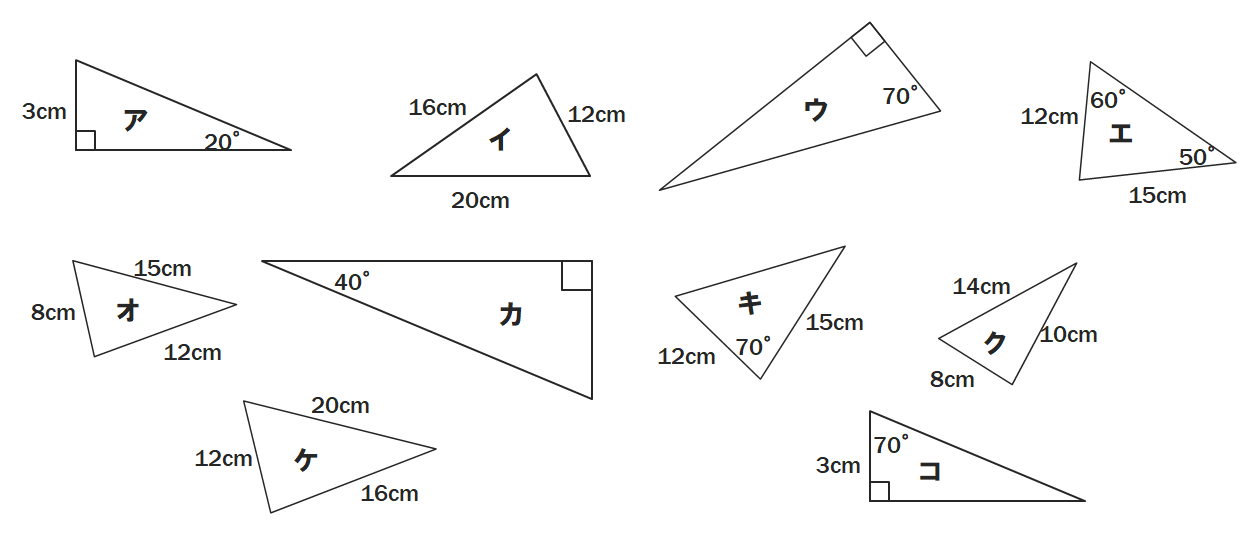



中2数学 3学期学年末テスト予想問題と解答解説 Pikuu
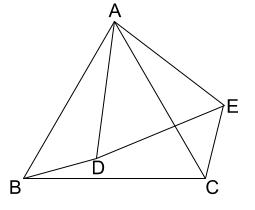



中学数学 正三角形の性質を利用した証明 中学数学の無料オンライン学習サイトchu Su



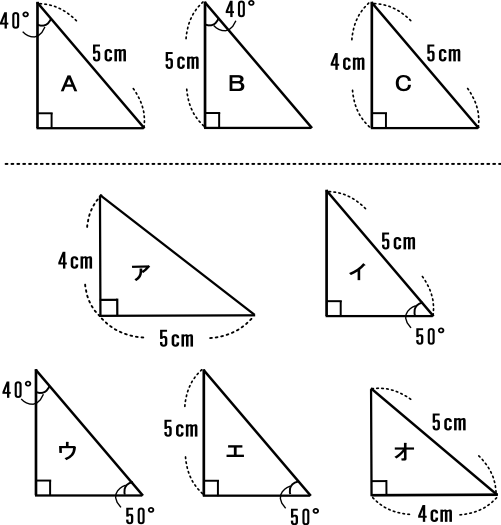
中学数学 証明 二等辺三角形であることの証明 中学数学の無料オンライン学習サイトchu Su



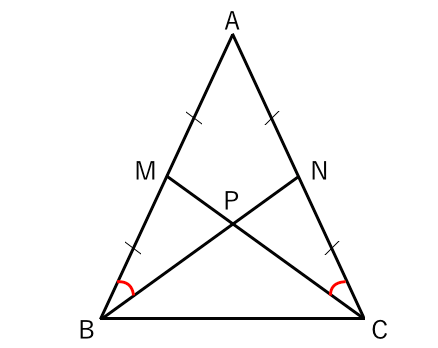
中学2年数学練習問題 直角三角形の合同条件と証明問題 図形と合同




中2 数学 中2 証明 中学生 数学のノート Clear




中学2年生 数学 合同と証明 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



中2数学 学年末テストの証明問題よく出るパターンをまとめてみた 個別指導塾のyou 学舎日記 公式ブログ




中2 証明 中二 中学生 数学のノート Clear



合同な図形 二等辺三角形の証明問題 苦手な数学を簡単に



中2数学 学年末テストの証明問題よく出るパターンをまとめてみた 個別指導塾のyou 学舎日記 公式ブログ




中学2年の数学 動画 証明チャレンジ Lv 6の問題 19ch



Http Www Fdtext Com Dat Suub2 4zukei 1kaku2 Pdf




中学3年 数学 東京書籍 新しい数学 相似な図形 平行線と比 赤城 ᐡᐤᐡ



0 件のコメント:
コメントを投稿